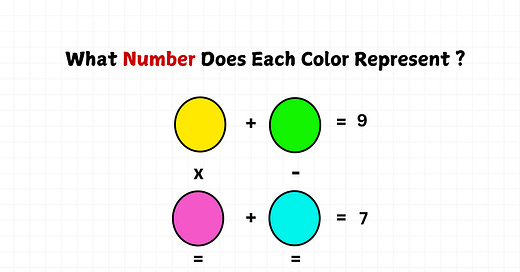What Number Does Each Color Represent?

A Fun Math Puzzle

Sep 23, 2024

A trial-and-error method often helps in problems like this. But not this time!

These are four circles of different colors, arranged in a 2x2 grid. The circles in the first row add up to give 9 and those in the second row add up to give 7.

Similarly, the product of the circles in the first column gives 36, and the difference of those in the second column gives 11.

Here’s the challenge: What numbers fit in appropriately in these circles?

Hint: Assign variables to each of the circles.

Feel free to get a pen and a paper and shoot at this puzzle. If you got the answers correctly, high five! You’re a math rock star, but stick around and see if our approach matches. If you don’t get the answer right, don’t sweat it, follow along!

Are you ready? Let’s dive in!

First of all, let us label each of these circles.

Let the yellow be y, the green be g, the pink be p, and the blue be b

With this, we can form a system of equations.

Here’s the trick! If we get one of the variables, getting other ones will be easier. If we get p for example, we can get y from eqn (iv), and b from eqn (ii). If we get y, we can also get g from eqn (i).

Let’s see how we can get p

To do this, we’ll work with equations (iv), (i), and (ii).

The goal here is to come up with an equation with one variable — p

Starting from (iv), y = 36/p

Let us replace this value in eqn (i)