This math puzzle may be a little tricky one, but if you remember your geometry well enough, you would have no problem.
Here’s the challenge: find the area of the large circle, given that the area of the small circle is 105m² and the triangle is an equilateral triangle.
If you can get the radius of the large circle, you would easily get its area! So, the ultimate goal is to find the radius of the large circle.
Hint: Form a right angled-triangle with the radii of both the small and large circles. Remember, 90–60–30 right-angled triangle is a special type of right triangle. One of its properties is that the hypotenuse is as twice as the shortest side of the triangle.
Feel free to get a pen and a paper and take a shot at this puzzle. If you found the answer to be 419.837m², high five! You’re a math rockstar, but stick around and see if our approach match up. If you don’t get the answer right, don’t sweat it, just follow along!
Are you ready? Let’s dive in!
To find the radius of the large circle, let us form a right-angled triangle with the radii of the circles (the circles share the same center).
Once this is done, one of the sides of the triangle would serve as the radius of the large circle and if we can find this side, then we’ve accomplished our mission. How cool?
Triangle AOB is a right-angled triangle and for a special triangle like the 90–60–30 right-angled triangle, OA is two times the length of OB.
Also, remember that the bigger triangle is an equilateral triangle. This means each of the angles is 60 degrees and when the radius of the large circle cuts through any of the angles in the triangle, we have 30 degrees for each.
We’re getting close to the finish line! r is the radius of the small circle and 2r is for the large circle — our target!
We can find r from the information we have — the area of the small circle is 105m².
The area of a circle is:
Where r is the radius of the circle.
So, for the small circle,
If we make r the subject of the formula, we would have r to be 5.7801m
Since the radius of the large circle is 2r, then it is 11.5601m — multiplying 5.7801m by 2.
We now have the radius of the large circle. Great!
We can now calculate its area with the formula given above. Substituting appropriately, we get this:
And there we go! The area of the large circle is 419.837m² 😊
Hope this was fun! Consider giving a few claps 👏 and a subscribe for more interesting math puzzles like this.










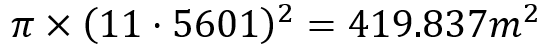
Hi, this is a really great puzzle, but your answer is technically incorrect: It should be exactly 420 sq. m. In fact, whatever the area of the smaller circle is, the area of the larger circle must always be exactly 4 times as large. You don't even need to calculate the radius; you only need to know that it will be doubled. This is why:
Area of smaller circle = pi * r squared
When the radius is doubled, we have:
Area of larger circle = pi * (2r) squared = pi * 4 r squared = 4 * pi * r squared.
So, the area of the larger circle = 4 * (pi * r squared) = 4 * (the area of the smaller circle).
If the area of the smaller circle is 105 sq. m. then the area of the larger circle must be 420 sq. m.
Your answer was very close to, but not quite, 420 because of rounding errors. If you keep more decimal places in your value of the radius, you will see that your answer gets closer to 420. The more decimal places you keep, the closer you get to the correct answer.