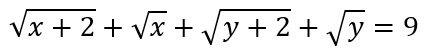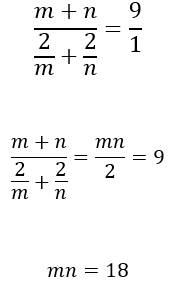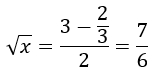Harvard Math Tournament Brain Teaser (2024)
Don't Try Solving This the Usual Way
Usually, when I see a pair of simultaneous equations like this — especially the kind where direct substitution or elimination won’t get you far — my first move is simple:
Add them. Subtract them. Maybe even both.
It’s a little trick that has saved me more times than I can count.
And this time?
It didn’t fail me either.
As soon as I looked closer, something interesting jumped out.
For this puzzle, the first step we’ll take is to add and subtract both equations, then do a bit of algebraic manipulation — and we’re good!
If you’ve got a smarter approach, I’d love to see it in the comments.
But for now…
Are you ready? Let’s jump in!
Adding these equations gives us:
Subtracting them gives:
We can bring them together!
What do you notice?
If you add and subtract the two equations, do you see a conjugate pattern forming on the left-hand side?
Cool!
This is where it gets more interesting.
To make things a little easier for us, from equation (i), let’s set m = √(x + 2) + √x, and n = √(y + 2) + √y
Also, multiplying the conjugates √(x + 2) + √x and √(x + 2) — √x gives us 2, and the same goes for √(y + 2) + √y and √(y + 2) — √y — thanks to the difference of squares identity.
So, when we divide 2 by m and by n, we get the terms on the left-hand side in equation (ii).
Now, we can rewrite equations (i) and (ii) as follows:
Beautiful!
Let’s try dividing equation (i) by equation (ii) and see what happens.
Only three pairs of numbers have a product of 18: (1,18), (2,9), and (3,6).
Now, considering equation (i), which says a + b = 9, only the pair (3,6) works — because 3 + 6 = 9.
This means that m = 3, and n = 6.
Also, we can say that 2√x = √(x + 2) + √x — (√(x + 2) — √x)
Making √x the subject of the formula, we get:
Remember, m = √(x + 2) + √x = 3, and
√(x + 2) — √x = 1 — (√(y + 2) — √y) = 1–2/n = 2/3
We can fix these right away!
To find the value of x, we square both sides.
This gives x = 49/36.
Thanks for reading! If you liked this puzzle, please give a few claps, follow me, and don’t forget to subscribe to stay updated with my latest articles.
You can also follow me on X (formerly Twitter) for more exciting challenges.
Feel free to reach out to me here. Let’s connect!