A Russian Math Olympiad Problem
Can You Find the Length of x?
Do you think you can find the length of X if the area of the square is 5m²?
What would be your approach?
Let us label a few points on this shape to make things a little easier for us.
Hint: Construct an imaginary semi-circle to make the shape a full circle, draw the circle's diameter to intersect with the chord CB, and apply the Intersecting Chords Theorem.
Feel free to get a pen and a paper and shoot at this puzzle. If you got the answer correctly, high five! You’re a math rock star, but stick around and see if our approach matches up. If you don’t get the answer right, don’t sweat it, just follow along!
Are you ready? Let’s dive in!
One way to find the solution to this problem is to use the Intersecting Chords Theorem to find line CD and the Pythagorean theorem to find line BD. If we get the lengths of both segments then we would simply add up to get the length of the chord.
How do we begin?
First of all, let’s get the line segment, BD. To do this, we can apply the Pythagorean theorem.
The area of the square is 5m². This means the length of each of the sides is the square root of 5. And this also means that line OD is the square root of 5.
To find BD, we need to know both OB and OD so we can use the Pythagorean theorem.
But how can we find OB?
Notice that OB = OE (since they both start from the origin and touch the circumference). If we find the value of OE, we have found OB.
We can achieve this if we see triangle DOE as a right-angled triangle and find the hypotenuse.
From here, OE is the square root of 10. This means OB is also the square root of 10.
Now, we have found the OB. Let us go ahead to find line BD. To do this, we need to apply to Pythagorean theorem, again.
We’re getting close to the finish line! 😊
Let’s find the line CD now.
To get this line segment, let us apply the apply the Intersecting Chords Theorem
According to the Intersecting Chords Theorem, if two chords intersect at a point inside a circle, then the product of the lengths of the segments of one chord equals the product of the lengths of the segments of the other chord.
In our case, we don’t have two chords intersecting. We only have a chord and a diameter. This theorem also applies provided they don’t intersect at the center.
This means, FD.DG = CD.BD
To continue with this, let us find FD.
Since OB is the square root of 10, this means OF is also the square root of 10, and OG is equal to the radius of 10 (the radius of the circle).
So, FD can be found if we subtract OD from OF.
DG can be found the same way:
Remember that BD is the square root of 15 and we’re yet to find CD.
We can get CD from this relationship: FD.DG = CD.BD
Now, we know CD. Great!
The sum of CD and BD gives us the length of the chord
By rationalizing the denominator, we have:
And there we go! We have found the length of the chord, BC 😊
Hope this was fun! Consider giving a like 👏 and a follow for more interesting math puzzles like this.
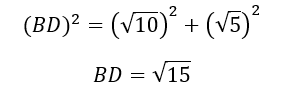
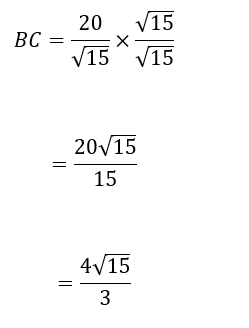
The problem statement didn't mention that the bottom-right corner of the square sits on the centre of the circle. Without that, assuming that OB = OE is unjustified.